There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
- For example, the pair
[0, 1], indicates that to take course0you have to first take course1.
You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether the course uj is a prerequisite of the course vj or not. Note that if course a is a prerequisite of course b and course b is a prerequisite of course c, then, course a is a prerequisite of course c.
Return a boolean array answer, where answer[j] is the answer of the jth query.
Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: course 0 is not a prerequisite of course 1 but the opposite is true.
Example 2:
Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites and each course is independent.
Example 3:
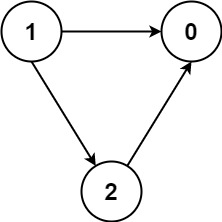
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]
Constraints:
2 <= numCourses <= 1000 <= prerequisite.length <= (numCourses * (numCourses - 1) / 2)0 <= ai, bi < nai != bi- All the pairs
[ai, bi]are unique. - The prerequisites graph has no cycles.
1 <= queries.length <= 1040 <= ui, vi < nui != vi
题意:你总共需要上 n 门课,课程编号依次为 0 到 n-1 。有的课会有直接的先修课程,比如如果想上课程 0 ,你必须先上课程 1 ,那么会以 [1,0] 数对的形式给出先修课程数对。
给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。对于每个查询对 queries[i] ,请判断 queries[i][0] 是否是 queries[i][1] 的先修课程,并返回一个布尔值列表,列表中每个元素依次分别对应 queries 每个查询对的判断结果。
解法1 多次BFS
矩阵范围很小,用邻接表存图,同时用 reachable[][] 二维数组存储可达性矩阵。然后对每门课程,BFS遍历和标记其后续课程,得到可达性矩阵。最后,对每个询问, O ( 1 ) O(1) O(1) 访问可达性矩阵得到答案。
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<int> g[numCourses];
for (const vector<int> &pre : prerequisites) g[pre[0]].push_back(pre[1]);
vector<vector<bool>> reachable(numCourses, vector<bool>(numCourses, false));
for (int i = 0; i < numCourses; ++i) {
queue<int> q;
vector<bool> vis(numCourses, false);
q.push(i);
vis[i] = true;
while (!q.empty()) {
int u = q.front(); q.pop();
reachable[i][u] = true; //由i可达u
for (const int &v : g[u]) {
if (!vis[v]) {
vis[v] = true;
q.push(v);
}
}
}
}
vector<bool> ans;
for (const vector<int> &q : queries) ans.push_back(reachable[q[0]][q[1]]);
return ans;
}
};
运行效率如下:
执行用时:196 ms, 在所有 C++ 提交中击败了96.01% 的用户
内存消耗:61.6 MB, 在所有 C++ 提交中击败了42.03% 的用户
解法2 Floyd算法
运用Floyd算法的思想进行动态规划:
class Solution {
public:
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
vector<vector<bool>> reachable(numCourses, vector<bool>(numCourses, false));
for (const vector<int> &pre : prerequisites) reachable[pre[0]][pre[1]] = true; //直接用邻接矩阵存储图
for (int k = 0; k < numCourses; ++k) {
for (int i = 0; i < numCourses; ++i) {
if (!reachable[i][k]) continue; //剪枝,i不可达k
for (int j = 0; j < numCourses; ++j)
reachable[i][j] = reachable[i][j] || reachable[k][j]; //i可达j或者i通过k可达j
}
}
vector<bool> ans;
for (const vector<int> &q : queries) ans.push_back(reachable[q[0]][q[1]]);
return ans;
}
};
由于是 O ( n 3 ) O(n^3) O(n3) 的动态规划,时间效率低很多:
执行用时:312 ms, 在所有 C++ 提交中击败了57.36% 的用户
内存消耗:57.7 MB, 在所有 C++ 提交中击败了75.46% 的用户
转载:https://blog.csdn.net/myRealization/article/details/116947696
