前言
Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…
这句话是著名大佬Knuth说的,也就是说虽然二分查找思路非常简单,但是实现的细节确实很费解。
好久没更新数据结构和算法的专栏了,既然学习了链表和顺序表,那么就可以讲一讲查找的算法了。我们会着重介绍二分查找的写法,因为虽然二分查找很好理解,但在实现的时候经常会因为边边角角的问题发生数组越界和查找错误的问题。
对了,我现在主要是用Java来编写程序了,其实和C语言在编写数据结构时大体结构是差不多的,只不过因为有GC所以不用再管释放内存的问题了;同时不再有结构体和指针了,取而代之的是对象和对象的引用。
顺序查找
顺序查找非常简单,对于无序的链表和数组结构,之前我们在实现Find()函数时就是使用的这种查找方式:从表中的第一个元素开始,挨个对元素和目标值进行比对,直到查找到相同元素。
基于数组结构的顺序查找:
public int Find(ElementType X){
NullException();
int P = 0;
while(P < Length() && SQList[P] != X){
++P;
}
if(P >= Length()){
System.out.println("No such Element in the list.list!");
return 0;
}
System.out.println("Element Find Success!");
return P+1;
}
基于链表结构的顺序查找:
private Node<ElementType> FindPrevious(ElementType X){
NullException();
Node<ElementType> P = Head;
while(P.Next != null && P.Next.Data != X){
P = P.Next;
}
if(P.Next == null){
System.out.println("No such Element in the list!");
return null;
}
return P;
}
在最好的情况下,要查找的刚好就是第一个元素;但是最坏情况下,也许查找的刚好就是最后一个元素,需要遍历整张表;如果查找未命中,也会遍历整张表。而平均下来需要n/2次查找,时间复杂度就是O(n)。
二分查找
二分查找首先是基于一个有序的数组的。为什么我们需要数组有序呢?从上面顺序查找的时间分析中我们知道,由于元素是无序排列的,所以我们并不能判断要查找的元素大概在什么位置,只能从头开始挨个找。
如果存放元素有序的,那么我们就能大概推测出要查找元素大致的位置,这样就可以极大地减少访问数组的次数了。另外如果要查找的元素不在存放元素区间内,也能马上就检查出来:如果比第一个元素小,或者比最后一个元素大,那么这个元素绝对不存在表中,直接未命中。而如果放在无序的表中则无法做到常数级时间内未命中。
解释完有序数组的优势,接下来来介绍二分查找这种常规的高效查找方式。二分查找每次通过将查询值与查询范围内的中间存储元素进行比较,下一次就在中间记录的左或者右边进行查找,也就是查询范围减半。重复这个过程,直到查找到或者最后范围只剩一个元素结束。简而言之,二分查找一次会筛选掉表中一半的数据。
递归实现
现在为了能够更好地理解二分查找,我们以一种独特的视角来观察,我会以图解的方式展现出来。我们假设一个很简单的数组,里面只放了7个从小到大排列的元素,然后我们需要查找的刚好是最后一个(事先是不知道的)。下面的图示展示了这一过程。
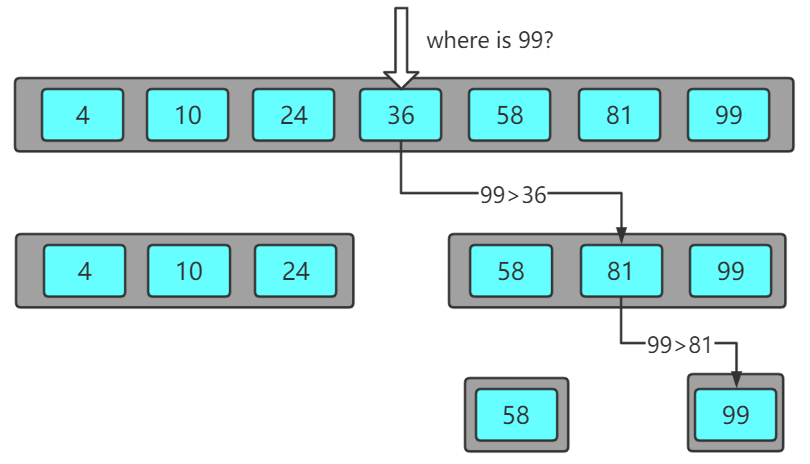
从图中其实可以看到,整个过程只用了3次就查找成功了。好,可能我的这幅图和其他讲解二分查找的博客里略有不同,不过没关系,后面会看到类似的图解,现在先关注于这幅图。除了跟踪查找路径之外,其实可以发现每一次查找时,我们都会将这个数组拆分为左右两部分,这就是关键了:每次进行二分查找时,我们都是在一个子数组里继续进行着查找,直到最后的子数组中只有一个元素为止。如果学习过树的朋友肯定不难发现,这和二叉树有着异曲同工之妙:每次搜索树其实就是不断进入它的子树进行查找。而且由于数组本身是有序的,所以左边元素肯定小于右边元素,也就是说如果将所有的搜索路径转化为一棵树时,这棵树还是一棵二叉搜索树!没错,二分查找的思想就是可以用二叉搜索树的思想来理解,因此可以使用递归的方法来实现它。
那么如何实现递归呢?在设计递归方法时,需要调用自身,因此需要对方法传入参数进行精心的设计。在二分查找中,每次递归调用后数组的查找范围将会减半,因此,递归方法调用时将会改变查找范围,这也就是递归方法需要传入的参数。如何表示查找的范围呢?简单啊,直接借用两个指针来表示查找范围的左右边界就行了,每次递归调用时将左或者右边界传入新的参数即可。如果觉得没讲明白那就看图吧。
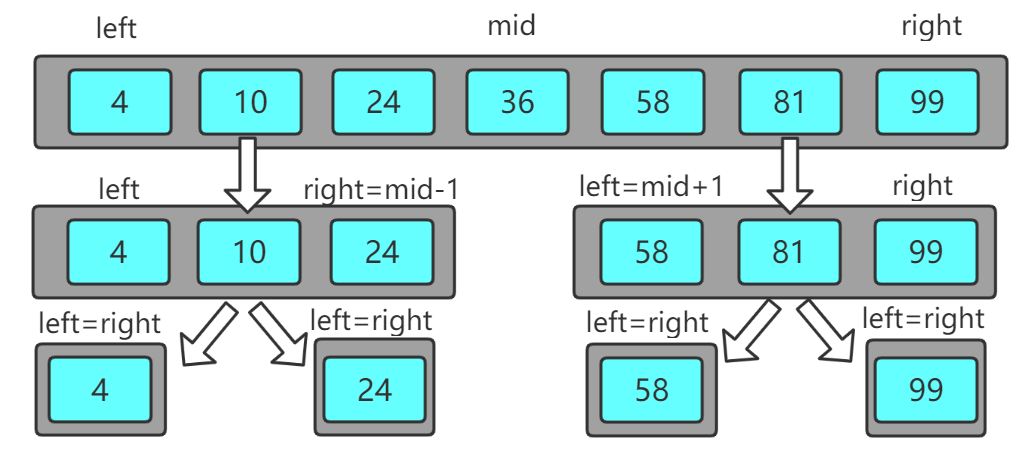
最后注意一定要有跳出递归的条件存在,在二分查找里,就是查找到值或者left>right了。相信过程已经非常清晰了,那么我们直接上代码:
public static int binarySearchRe(int[] arr,int key){
int left = 0;
int right = arr.length-1;
int i = binarySearchRe(arr,key,left,right);
return i;
}
private static int binarySearchRe(int[] arr,int key,int left,int right){
//返回-1表示查找未命中
if(left>right){return -1;}
int mid = (left+right)/2;
if(arr[mid]<key){ return binarySearchRe(arr,key,mid+1,right); }
else if(arr[mid]>key){ return binarySearchRe(arr,key ,left,mid-1); }
else { return mid; }
}
总的来说没有大的问题,有一个小问题后面再来讨论。
循环实现
递归好是好,就是数据量一大就容易Stack Overflow了。所以虽然个人认为递归的写法既好理解又好记,但是循环实现才是平时更加常用的。通常要用循环来实现递归还需要借助栈结构,但是二分查找不需要,代码也很简单。
从递归的代码我们可以轻易看出,其实每次的判断条件就是mid位置的元素与查找值key作比较,因此,只要循环内mid的值随着查找范围减小而变化就可以了。而mid的值由两个变量影响:left和right,所以只要改变它们的值就可以在下一轮循环中重新计算mid了。直接将left或者right在每次查找后赋值为当前mid的前后位置(mid±1)即可实现改变查询范围的想法了,这一方式在本质上和递归是一样的,递归只不过是把赋值变成了传参罢了。
public static int binarySearch(int[] arr,int key){
int left = 0;
int right = arr.length-1;
int mid;
while(left <= right){
mid = (left+right)/2;
if(arr[mid] < key){ left = mid+1;}
else if(arr[mid] > key){ right = mid-1;}
else {return mid;}
}
return -1;
}
各种变体
关于二分查找的变体有很多,这里主要介绍常用的两种情况。上面的例子中数组中存放的元素是不同的,但是在更加一般现实的场景下,也许是有多个相同的元素(键值)存在,而需要查找的元素刚好有多个,这个时候我们可能会有两种要求:1.查找返回第一个;2.查找返回最后一个。
要实现这样的需求其实只需要在原有代码上稍作一些修改即可,不过我们首先还是先搞明白如何做到。以第一个为例,具体的流程我作了一张图:
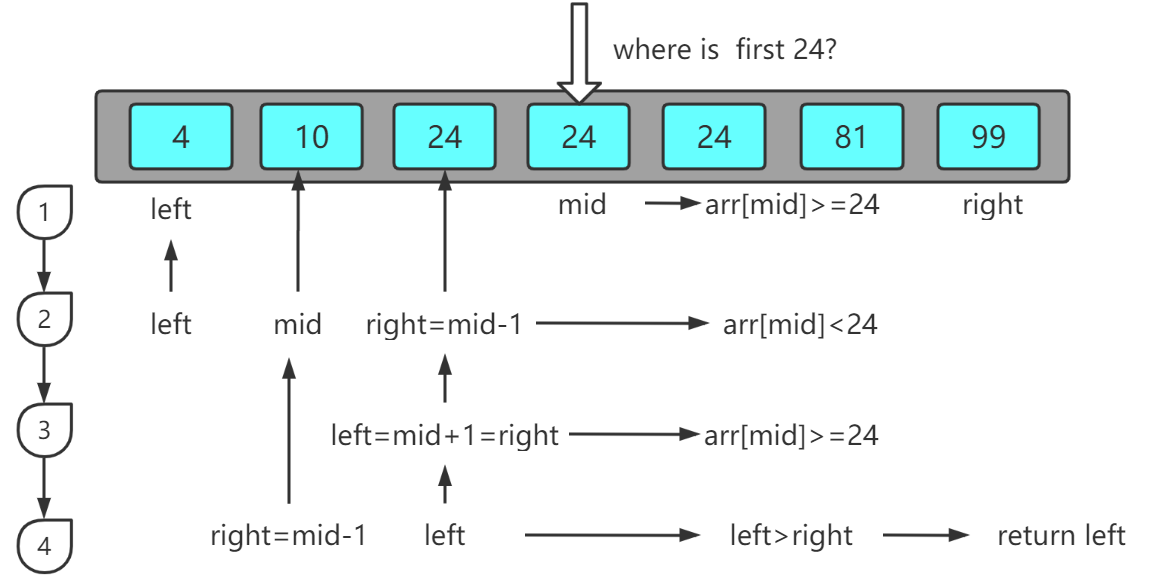
这次我们的数组中有三个值为24的元素,而要求找到第一个24。第一次查找时,发现中间值与查找值key相等,但是并不一定是第一个,所以不能直接像上面代码一样直接返回,而是继续进行二分查找。那么这里是该查前半部分还是后半部分呢?图上我们可以很直观地看出应该是查前半部分,所以当中间元素不小于查找值时查找范围为前半部分,right指针移动。接着第二次查找中间值小于查找值key,left指针移动;第三次查找right指针再次移动;当第四次循环时,发现left>right,同时left所在位置刚好就在返回位置,因此跳出循环,返回left即可。
有人可能会问那如果刚好第一次查询到的就是要返回的值,那么后面一直查前半部分不是就查不到了吗。其实不用担心,因为如果是这样,那么之后的查询right将永远停留在返回元素之前一个位置,而最后left会逐渐增加至right后的位置,也就是要返回元素的位置,然后查找成功。
上面只是简单地举个例子,换成其他数量和分布的元素都能够成功查找到。通过归纳可以发现:最后每次的返回位置都恰好是left停留的位置。仔细想想其实也很合理,这里可以得出这样的规律:
- 判断循环的条件就是left<=right的,因此跳出循环时肯定是left>right。
- left只会不断向后增加,right则是不断向前减小。(跟踪图上的left和right的轨迹就可以发现)
- 每次中间值小于查找值key时left才增加,因此left只要移动到指定值元素就不会再变化。
- left每次都会等于mid后面一位的元素,该元素不小于mid上的元素,left移动到再也不动的位置肯定就是最后要返回的位置。
通过一顿总结归纳,我们就可以开始写代码了。
public static int binarySearchFirst(int[] arr,int key){
int length=arr.length-1;
int left=0;
int right=length;
int mid;
while(left<=right){
mid = (left+right)/2;
if(arr[mid] < key){ left=mid+1; }
else { right=mid-1; }
}
//both conditions should be satisfied
if(left <= length && arr[left] == key) {
return left;
}
return -1;
}
注意上面代码第9行的判定条件,是不包含等号。其他博客可能会有不同的写法,但其实都是一样的,只不过条件和left和right操作对调了一下位置。请记住条件和内部的执行操作不要搞混淆了。
那么第二个要求呢?了解了上面的规律和总结,那么第二个要求其实也迎刃而解了,只需要稍微改动一下即可。具体就不画图了(偷个懒),直接文字描述区别吧:
- 和第一个要求不同,当中间值等于key右半部分。即当中间元素不大于查找值时查找右半部分,left指针移动。反之,right指针移动。
- 到最后,每次中间值大于查找值key时right才减小,而每次都会等于mid前面一位的元素,该元素不大于mid上的元素,因此right移动到再也不动的位置肯定就是最后要返回的位置。
理解了上面的区别,接下来代码就好说了,只有一点点的改动。
public static int binarySearchLast(int[] arr,int key){
int length=arr.length-1;
int left=0;
int right=length;
int mid;
while(left<=right){
mid = (left+right)/2;
if(arr[mid] <= key){ left=mid+1; }
else { right=mid-1; }
}
//both conditions should be satisfied
if(right >= 0 && arr[right] == key) {
return right;
}
return -1;
}
在跳出循环之后一定要检查一下left或者right是否在数组范围内,不然返回的值就有可能出现越界的情况,而且如果越界那就说明这个元素是不存在于这个数组的。
同时我们之前的假设都是基于查找值key存在于数组的条件,然而实际上也有可能查找未命中的,所以还要检查一下该位置元素是不是等于查找值。
细节优化
其实能够记住上面的代码并手写出来那么也OK了,不过精益求精,我们来看看上面的代码还有哪些细节上可以优化的地方。
第一个问题是在mid计算这里,如果数组非常庞大,left和right非常巨大时,它们相加就会超出int(Integer)的最大值,造成溢出。所以为了防止这种情况出现,可以将mid的计算改为:mid=left+(right-left)/2 。这个问题其实存在了20年都没被发现。
第二个问题是,我们发现用之前的写法来查找时,如果mid元素是不小于查找值key的时候,一次循环是需要两次比较的;而小于查找值key时只需要一次比较。那么查找值key为数组中较为靠后的元素时将会比查找靠前的元素花费更多的时间,如果用二叉查找树的说法来说就是这棵树不是完美平衡的。
要解决这个问题那么就要对边界条件和进行一定的改造,使得向左向右每次比较次数都只需要一次。怎么改造,emmm,其实要讲起思路还蛮复杂,那就又可以写一篇文章仔细品味了,Knuth 大佬想必就是说的下面这种写法令人费解吧。这里先说下大致的做法吧:
- 查找范围改为左闭右开的[left,right);
- mid元素不小于查找值时right=mid,而不是mid+1;
- 最后返回left或者right都可以。
具体代码如下:
public static int binarySearch(int[] arr,int key){
int left = 0;
int right = arr.length-1;
int mid;
while(left < right){
mid = left+(right-left)/2;
if(arr[mid] < key){ left = mid+1;}
else { right = mid; }
}
return left;//or right
}
这段代码返回的是[left,right)内第一个不小于key元素的位置,因为在实际应用当中,如果查找未命中那么就要准备插入这个数据了,插入的位置就应该是这个地方。要完全理解这段代码其实并不容易,不过实在不行就记住它吧。
时间复杂度分析
学习过二叉查找树的同学肯定都知道它的时间复杂度是O(logn),二分查找由于其原理与二叉树类似,因此时间复杂度也是如此。不过我们还是用数学的方法来进行推算吧:
我们之前也说过,二分查找每次回排除掉一半不适合的值,所以当有n个元素时:
第一次查找剩下:n/2;
第两次查找剩下:n/2/2 = n/4;
第m次查找剩下:n/(2m);
而二分查找是在排除到只剩下最后一个值之后得到结果,即n/(2m)=1;
解得:m=log2n。所以时间复杂度为O(log n)。
但要向有序数组中插入新元素最坏情况下需要访问约2n次数组(先插入到第一个位置,元素全部向后移动;然后排序到最后,元素全部又向前移),因此构建一个有序数组(即插入n个元素到空表中)需要访问约n2次数组。
总结
我万万没想到写个二分查找居然都让我花费了这么多心思和时间。虽然只是一个很简单的知识点,但是仔细抠细节就会发现还是有很多地方值得深入探讨的。所以看我写的这么详细的份上给个赞呗!
参考资料
- 《算法(第四版)》
- 知乎—二分查找有几种写法?它们的区别是什么?
- 简书—你真的了解二分查找吗?
转载:https://blog.csdn.net/weixin_44982066/article/details/106296252
